Asymptotics Problems Solutions #

1. False. Worst case can be O(N)
2. False. Worst case can be O(N)
3. False. Can be O(log(N)), so a tight bound is not true
4. True
5. True, as it is O(N)
6. False. These slides indicate that after N random insertions, the average depth of the tree is ~ 2(ln(N)), which implies that a single containsKey call after the insertions will indeed take ~ 2(ln(N)). However, the question asks for the average total number of comparisons for all the inserts and all the containsKey, which is significantly more than ~ 2(ln(N)).
7. False. In the best case, these nodes are near the root. Note that if C, K are randomly chosen, then this is True on average, since the depth of the average node in the tree is given by the sum
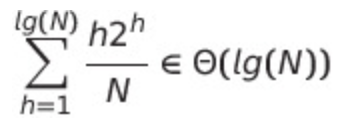
8. There are no conditions on the tree, so we must consider when the tree is bushy, left-spindly, and right-spindly.
   • Bushy Tree: For any z, we see that going down either recursive path approximately reduces the problem size by half, giving O(NlgN)
   • Spindly Tree (Left): Best-case runtime occurs when we recurse on the right subtree (z == N), giving O(N) runtime. Worst-case runtime occurs when we recurse on the left subtree as far as possible (z == 1), giving O(N2)
   • Spindly Tree (Right): Best-case runtime occurs when we recurse on the left subtree (z == 1), giving O(N) runtime. Worst-case runtime occurs when we recurse on the right subtree as far as possible (z == N), giving O(N2)

   The question asks us to give an O bound. By inspection of the above cases, we have that this method is O(N2).